A Uniformly Continuous and Differentiable Function Implies Bounded Derivative

Uniform Continuity

When we defined continuity, it was a local notion. Even when defining continuity on a set, we did it by checking continuity at every point of the set individually. There is also a purely global notion that strengthens continuity.

Definition.
Let f be a function, let M be a subset of its domain D(f ). We say that f is uniformly continuous on M if for every ε > 0 there exists δ > 0 such that for all a,x from M satisfying |x −a| < δ we have |f (x) −f (a)| <ε.

This is almost the same as the definition of continuity we saw, there is one crucial difference though. If we wanted to show ordinary continuity on M, we would start by fixing a point a from M and then we would show that we can win every epsilon-delta game. That is, we play the game independently for every point, which means that for the same given epsilon we have the freedom of choosing different deltas for different points. For uniform continuity we play the game simultaneously for all points from M. Given one particular tolerance, we want to find delta so that it wins this epsilon-game at all points a from M.

Example: Consider the function f (x) = 1/x. We know that it is continuous on (0,∞). However, it is not uniformly continuous on this interval. Indeed, in the picture we tried to show that given a certain epsilon, we are forced to make delta smaller and smaller to win games for this epsilon as we move closer to 0 with a and it seems that this process does not stop, no delta will work universally.

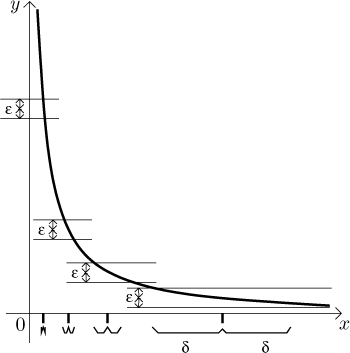
On the other hand, if we restrict ourselves just to the interval [1,∞), this function is already uniformly continuous there. The delta we find "at the left end" will work everywhere.

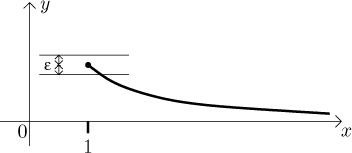
We can look at it from another point of view. If we decide to make steps of a certain length, then in the second situation, no matter where we make such a step, the function always grows or falls by an amount that does not exceed certain universal quantity. In other words, for a uniformly continuous function, given the size of a step, we can make a global upper estimate of how much the function changes, no matter where we make that step in the given set. On the other hand, in the first picture we see that if we start making even very small steps closer and closer to 0, the function will jump by more and more, without any bound for such jump.

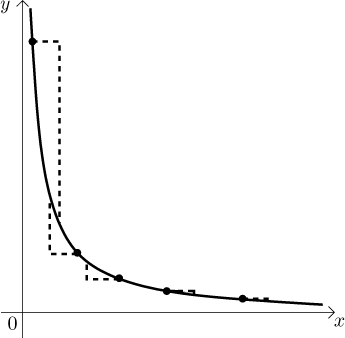
In fact, the point a stops being special, we deal with pairs of points. Thus we can restate the definition in this way. A function is uniformly continuous on a given set if, given a bound epsilon, we can find a delta so that any two points from the set that are near enough (closer than delta) when substituted into the function will not cause a jump larger than the given epsilon.

As the name and the above paragraphs suggest, uniform continuity is more than continuity.

Theorem.
A uniformly continuous function on a set is necessarily continuous on that set.

On the other hand, the above exampe shows that not every continuous function is uniformly continuous. Even boundedness would not help, the function sin(1/x) is bounded and continuous on the bounded interval (0,1), yet it is not uniformly continuous, since it has infinitely many waves of height 2 squeezed next to the origin, which means that with even very (arbitrarily) tiny steps one can go from the top of one wave to the bottom of another (see sin(1/x) in Theory - Elementary function).

There are several ways to recognize uniformly continuous functions without hunting for deltas.

Theorem.
A function that is continuous on a bounded closed set is necessarily uniformly continuous on that set.

Note that both conditions on the set are needed. The function 1/x is not uniformly contiuous even on the bounded set (0,1). For an example on an unbounded closed set we may consider x ² on [0,∞), uniform continuity fails in a similar way as in the above example, just there we had problems around 0, now with x ² the speed of growth keeps increasing as we go to infinity.

Theorem.
If a function is continuous on an interval, differentiable in its interior and the derivative is bounded there, then the function is uniformly continuous on that interval.

Note that the condition on boundedness of derivative is not necessary, because there are uniformly continuous functions whose derivative in not bounded on the set of uniform continuity. One such example is the root of x on [0,1].

Uniformly continuous functions are nicer to work with. However, this is somewhat beyond the scope of Math Tutor, so we leave it here.

---

Back to Theory - Real functions

santiagopritter.blogspot.com

Source: https://math.fel.cvut.cz/mt/txtb/3/txe3ba3g.htm